免费自己做网站吗武汉seo首页优化公司

平衡二叉树是啥我就不多说了，本篇博客只讲原理与方法。

首先引入平衡因子的概念。平衡因子（Balance Factor），以下简称bf。

bf = 右子树深度 - 左子树深度。平衡结点的平衡因子可为：-1，0，1。除此之外的结点都需要调整。

如下图：

AVL树的基础创建

创建AVL树的基本架构与二叉搜索树的创建基本一样，不同是为了方便后续的旋转与平衡因子的改变，多引入bf与parent记录结点的平衡因子与该结点的父节点，形成三叉链。

AVL树的旋转

右单旋

新节点插入较高左子树的左侧

以上过程可以简单的看作是30的右子树变成60的左子树，60变成30的右子树。其中h高度可以取值为0。

这是两种不同的情况。不同点在于30的右子树为NULL，此时并不需要更新其子树的parent结点的指向。每个结点的bf统统归零。

左单旋

 新节点插入较高右子树的右侧

以上过程可简单看成，60的左变成30的右，30变成60的左。其中60的左可以为空。

和右单旋同理。

先左单旋再右单旋（LR）

新节点插入较高左子树的右侧

路径可以形象的看作“<”先左后右（LR）

将双旋变成单旋后再旋转，即：先对30进行左单旋，然后再对90进行右单旋，旋转完成后再
考虑平衡因子的更新。

平衡因子的更新

情况一：如上图在b处插入后60结点的bf=-1，最终平衡树的平衡因子为60：0，30：0，90：1。

情况二：

在c处插入后60结点的bf=1,最终平衡因子为30：-1，60：0，90：0。

情况三：

插入60结点，60结点bf=1，最终平衡因子为30：0，60：0，90：0。

先右单旋再左单旋（RL）

新节点插入较高右子树的左侧

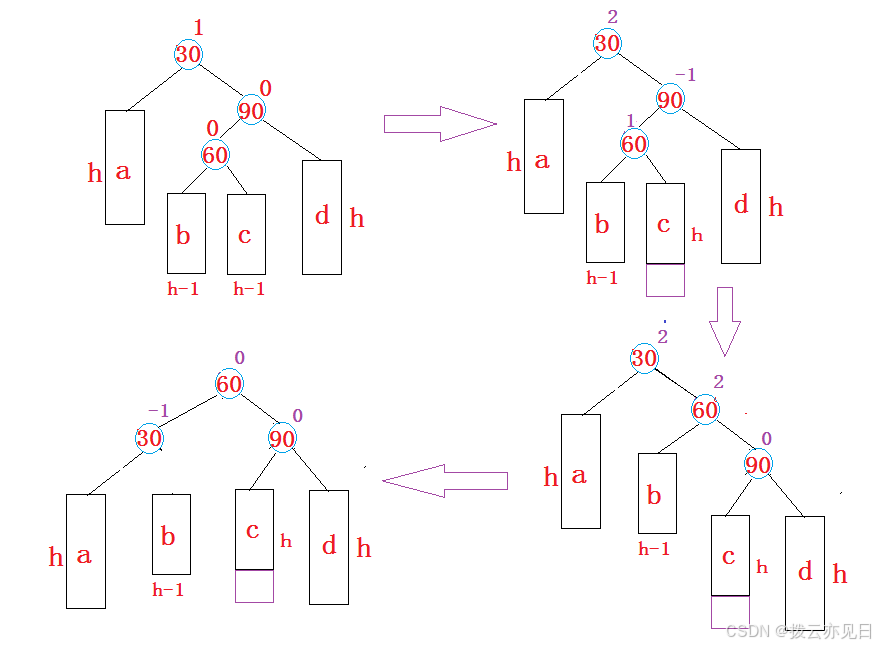
路径可以形象看作“>’，先右后左（RL）。

将双旋变成单旋后再旋转，即：先对90进行左单旋，然后再对30进行右单旋，旋转完成后再
考虑平衡因子的更新。

平衡因子讨论和LR类似。

代码

#pragma once
#include <iostream>
#include <stdlib.h>
using namespace std;template <class K,class V>
struct AVLtreeNode {AVLtreeNode<K, V>* _right;AVLtreeNode<K, V>* _left;AVLtreeNode<K, V>* _parent;AVLtreeNode(const pair<K,V>& kv):_right(nullptr),_left(nullptr),_parent(nullptr),_kv(kv),_bf(0){}int _bf; //平衡因子pair<K, V> _kv;
};
template <class K,class V>
class AVLtree {typedef AVLtreeNode<K,V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){//不影响break;}else if (parent->_bf == 1 || parent->_bf == -1){//高度变了，需要继续向上计算平衡因子cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//parnet所在的子树出现不平衡，需要旋转if (parent->_bf == 2){if (cur->_bf == 1){RotateL(parent);}else if (cur->_bf == -1){RotateRL(parent);}}else if (parent->_bf == -2){if (cur->_bf == -1){RotateR(parent);}else if(cur->_bf==1){RotateLR(parent);}}break;}}return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;Node* node = parent->_parent;parent->_parent = subR;//1、原来parent是这棵树的根，现在subR是根//2、parent不是根，parent还有他自己的_parent，现在让_parent指向subRif (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (node->_left == parent){node->_left = subR;}else{node->_right = subR;}subR->_parent = node;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subL->_right;Node* node = parent->_parent;subL->_right = parent;if (subLR) subLR->_parent = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parent == node->_left){node->_left = subL;}else{node->_right = subL;}subL->_parent = node;}subL->_bf = parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first <<" : " << root->_kv.second << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}int Height(Node* root){if (root == nullptr) return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool _IsBalance(Node*root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return abs(leftHeight - rightHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}bool IsBalance(){return _IsBalance(_root);}private:Node* _root=nullptr;
};void TestAVLTree()
{int a[] = { 16,3,7,11,9,26,18,14,15 };AVLtree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;
}