让人做网站需要注意什么百度高级检索入口

一、题目描述

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

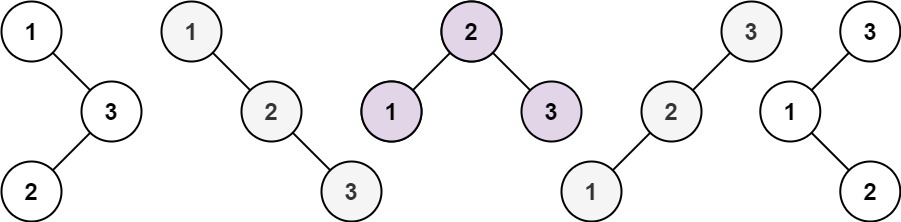
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 8

二、解题思路

我们可以使用递归的方法来解决这个问题。递归的基本思想是，对于每个数i，作为根节点，其左子树由[1, i-1]构成，其右子树由[i+1, n]构成。对于左子树和右子树，我们又可以应用同样的方法来生成所有可能的BST。

1. 递归基准情况: 如果n小于1，那么没有节点可以用来构建树，返回空列表。
2. 递归分解: 对于每个数i，作为可能的根节点，递归地为左子树和右子树生成所有可能的BST。
3. 合并结果: 对于每个根节点i，我们需要将所有可能的左子树和右子树进行组合，得到所有可能的BST。

三、具体代码

import java.util.List;
import java.util.ArrayList;public class Solution {public List<TreeNode> generateTrees(int n) {if (n == 0) {return new ArrayList<>();}return generateSubtrees(1, n);}private List<TreeNode> generateSubtrees(int start, int end) {List<TreeNode> subtrees = new ArrayList<>();if (start > end) {subtrees.add(null); // 添加空树作为递归基准情况return subtrees;}for (int i = start; i <= end; i++) {// 生成所有可能的左子树List<TreeNode> leftSubtrees = generateSubtrees(start, i - 1);// 生成所有可能的右子树List<TreeNode> rightSubtrees = generateSubtrees(i + 1, end);// 将左子树和右子树与根节点i组合for (TreeNode left : leftSubtrees) {for (TreeNode right : rightSubtrees) {TreeNode root = new TreeNode(i);root.left = left;root.right = right;subtrees.add(root);}}}return subtrees;}
}

四、时间复杂度和空间复杂度

1. 时间复杂度

时间复杂度的分析基于每个节点作为根节点时，生成所有可能的左子树和右子树的组合。

• 对于每个节点i作为根节点，左子树的可能数为i-1，右子树的可能数为n-i。

• 对于每个节点i，我们需要进行(i-1)*(n-i)次操作来生成所有可能的左子树和右子树的组合。

• 因为我们需要对1到n的每个数都作为根节点进行这样的操作，所以总的时间复杂度为：

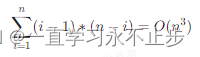  这是因为对于每个节点i，我们都在进行近似n^2次操作，而这样的操作要进行n次。

因此，时间复杂度是O(n^3)。

2. 空间复杂度

空间复杂度的分析基于递归调用栈的深度以及存储所有生成的树结构的空间。

（1）递归调用栈的深度：递归调用栈的最大深度是O(n)，因为每次递归都会减少一个数字直到没有数字剩余。

（2）存储所有生成的树结构的空间：

• 总共有卡特兰数C(n)个不同的二叉搜索树。
• 每个树的结构最多有O(n)个节点。
• 因此，总的空间复杂度是O(n) * C(n)。

卡特兰数C(n)的增长速度是O(4^n / n^1.5)，所以总的空间复杂度是O(n) * O(4^n / n^1.5) = O(4^n / n^0.5)。

因此，该算法的时间复杂度是O(n^3)，空间复杂度是O(4^n / n^0.5)。

五、总结知识点

1. 递归：代码中使用了递归函数generateSubtrees来生成所有可能的二叉搜索树。递归是一种常用的算法设计技巧，它允许函数调用自身来解决问题的一个较小部分，直到达到一个基准情况。

2. 二叉搜索树（BST）的性质：二叉搜索树是一种特殊的二叉树，其中每个节点的值都大于其左子树的所有节点的值，且小于其右子树的所有节点的值。代码中利用了这个性质来生成所有可能的BST。

3. 列表（List）的使用：Java中的List接口用于存储有序的集合，代码中使用了ArrayList来实现这个接口。列表用于存储生成的子树和最终的树集合。

4. 循环和条件语句：代码中使用了for循环来遍历可能的根节点值，并使用了if语句来判断递归的基准情况。

5. 树的结构：代码中定义了TreeNode类来表示树的节点，每个节点包含一个值和指向其左右子节点的引用。

6. 动态规划思想：虽然代码中没有显式地使用动态规划，但是递归方法中隐含了动态规划的思想，即通过解决子问题来构建整个问题的解决方案，并且存储这些子问题的解以避免重复计算。

7. 函数定义和返回值：代码中定义了两个函数：generateTrees是公共接口，generateSubtrees是私有辅助函数。generateSubtrees函数返回一个包含所有可能的子树的列表。

8. 空树的处理：在递归的基准情况中，代码添加了一个空树（null）到子树列表中。这表示没有更多的节点可以用来构建树，是递归终止的条件。

9. 组合问题的解决：代码通过两层循环来组合左子树和右子树，这是一种常见的解决组合问题的方法。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。