做网站客户尾款老不给怎么办丽水网站seo

摘要：总结一些前端算法题，持续更新！

一、数据结构与算法

时间复杂度-程序执行时需要的计算量（CPU）

空间复杂度-程序执行时需要的内存空间

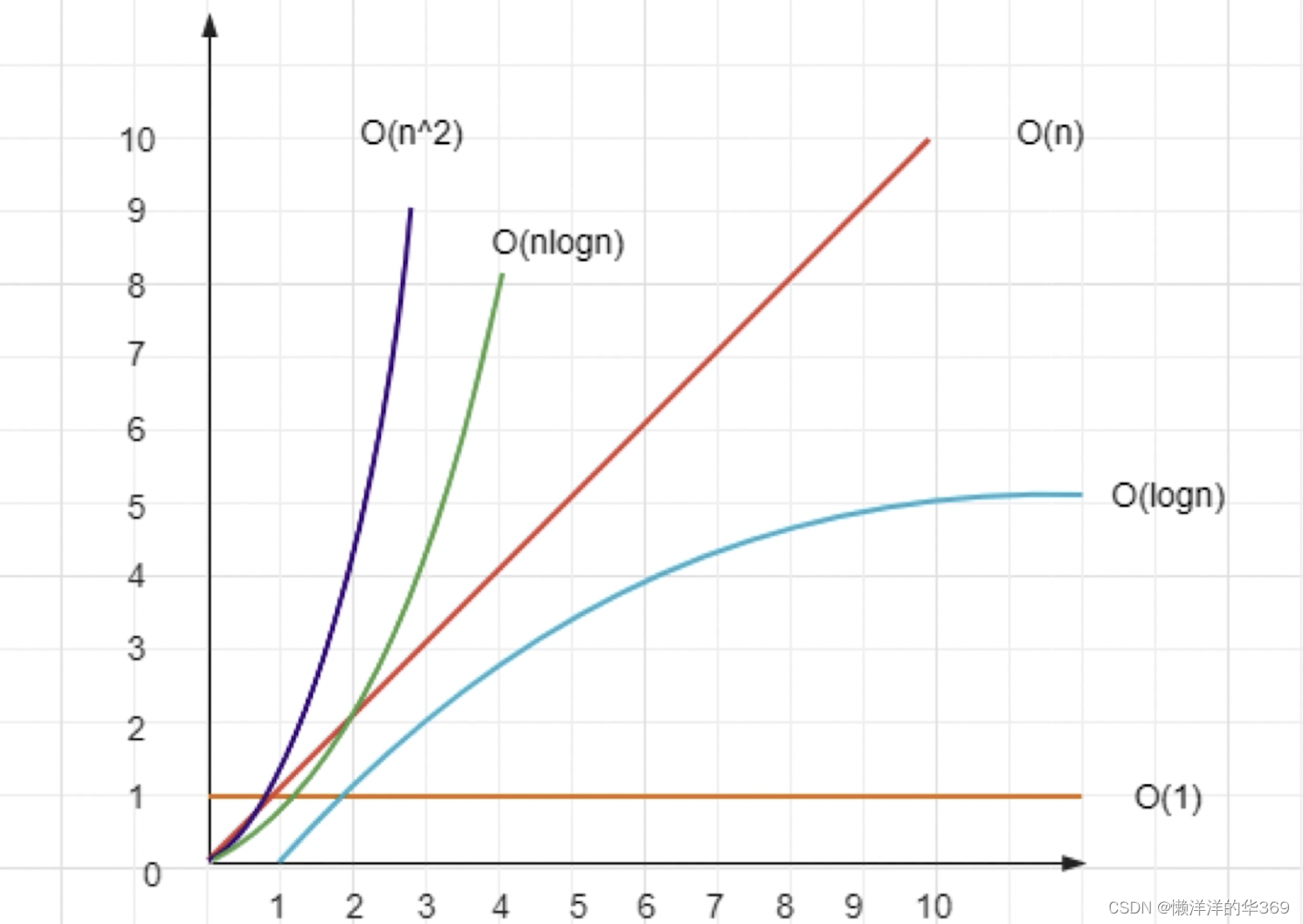
前端开发：重时间，轻空间

1.把一个数组旋转k步

array = [1, 2, 3, 4, 5, 6, 7] 旋转数组k=3， 结果[5, 6, 7, 1, 2, 3, 4]

思路1：把末尾的元素挨个pop，然后unshift到数组前面；

思路2：把数组拆分，最后concat拼接到一起

/**
* 旋转数组k步使用pop和unshift
*/
function rotate1(arr: number[], k: number): number[] {const length = arr.lengthif (!k || length === 0) returnconst step = Math.abs( k%length)   // abs 取绝对值,k不是数值是返回NaN// 时间复杂度o(n^2), 空间复杂度o(1)for (let i = 0; i<step; i++) {    // 任何值与NaN做计算返回falseconst n = arr.pop()if (n != null  ) {arr.unshift(n)  //数组是一个有序结构，unshift操作会非常慢！！！O(n);splice和shift也很慢}}return arr
}
/**
* 旋转数组k步使用concat
*/
function rotate2(arr: number[], k: number): number[] {const length = arr.lengthif (!k || length === 0) returnconst step = Math.abs( k%length)   // abs 取绝对值const part1 = arr.slice(-step)  // O(1)const part2 = arr.slice(0,length-step)// 时间复杂度o(1), 空间复杂度O(n)return part1.concat(part2)
}

常见内置API中的复杂度：

• unshift: unshift 方法将给定的值插入到类数组对象的开头，并返回新的数组长度。时间复杂度为 O(n)，其中 n 是数组的长度，因为在插入时需要将原有的元素逐一往后移动一位；空间复杂度为 O(1)。
• splice: splice 方法用于从数组中添加或删除元素，并返回被删除的元素组成的新数组。splice 的时间复杂度为 O(n)，其中 n 是数组的长度，因为在删除或插入元素后，需要移动数组中的其他元素以保持连续性；空间复杂度为 O(n)，因为需要创建一个新的数组。
• shift: shift 方法用于从数组的开头删除一个元素，并返回被删除的元素。shift 的时间复杂度为 O(n)，其中 n 是数组的长度，因为在删除元素后，需要将数组中的其他元素往前移动一位以保持连续性；空间复杂度为 O(1)，因为不需要额外的空间来存储。
• concat: concat 方法用于将两个或多个数组合并成一个新数组。时间复杂度为 O(1)，数组末尾操作；空间复杂度为 O(n+m)，m、n是原数组长度，因为新的数组需要存储。
• slice: slice 方法用于从数组中提取出指定范围的元素，并返回一个新数组（不改变原数组）。时间复杂度为 O(1)；空间复杂度为 O(n)，因为需要创建一个新的数组来存储提取的元素。

2.判断字符串是否为括号匹配

一个字符串s可能包括{}()[]三种括号，判断s是否是括号匹配

考察的数据结构是栈，先进后出；ApI: push pop length

栈 VS数组区别

栈：逻辑结构；理论模型，不管如何实现，不受任何语言限制

数组：物理结构；真实功能实现，受限于编程语言

/**
* 判断是否括号匹配
*/
function matchBracket(str: string): boolean {const length = str.lengthif(length === 0) return trueconst stack = []const leftSymbols = '{[('const rightSymbols = '}])'for (let i = 0; i <length; i++) {const s = str[i]if (leftSymbols.includes(s)) {stack.push(s)  // 左括号，压栈} else if (rightSymbols.includes(s)) {// 左括号，判断栈顶（是否出栈）const top = stack[stack.length-1]if (isMatch(top, s)) {stack.pop} else {return false}}}return stack.length === 0
}
/**
* 判断左右括号是否匹配
*/
functionn isMatch(left: string, right: string): boolean {if (left === '{' && right === '}') return trueif (left === '[' && right === ']') return trueif (left === '(' && right === ')') return truereturn false
}

        时间复杂度O(n); 空间复杂度O(n)

3.定义一个JS函数，反转单向链表

        链表

        链表是一种物理结构（非逻辑结构）， 类似于数组

        数组需要一段连续的内存空间，而链表是零散的

        链表节点的数据结构{value, next?, prev?}

        链表 VS 数组

        都是有序结构（Set是无序的）

• 链表：查询需要遍历元素慢O(n)， 新增和删除不需要移动其他元素很快快O(1);
• 数组：按照索引查询快时间复杂度O(1), 新增和删除需要移动其他元素比较慢慢O(n)；
• 数组适合随机访问元素、大小固定的情况，而链表适合频繁的插入或删除操作、大小不确定的情况

/**
*  反转单项链表
*/
interface ILinkListNode {   // 定义类型value: number    // 类型结构，value、next?next?: ILinkListNode   //?表示next是可选的
}/**
*  反转单向链表，并返回反转之后的head node
*/
fucntion reserveLinkList(listNode: ILinkListNode): ILinkListNode {// 定义三个指针let prevNode: ILinkListNode | undefined = undefinedlet curNode: ILinkListNode | undefined = undefinedlet nextNode: ILinkListNode | undefined = listNode// 以nextNode为主，遍历链表while(nextNode) {// 第一个元素，删掉next，防止循环引用if (curNode && !prevNode) {delete curNode.next}// 反转指针if (curNode && prevNode) {  中间状态，指针都有值curNode.next = prevNode}// 指针后移prevNode = curNodecurNode = nextNodenextNode = nextNode?.next   //有nextNode.next则返回，否则返回空    } // 最后一个元素：当nextNode空时， 此时curNode尚未设置nextcurNode!.next = prevNodereturn curNode!
}/**
*  根据数组创建单项链表
*/
function createLinkList(arr: number): ILinkListNode {const length = arr.lengthif (length === 0) throw new Error('array is Empty')let curNode: ILinkListNode = {value: arr[length-1]}if (length == 1) return curNodefor ( let i = length-2; i >=0; i--) {curNode = {curNode = {value: arr[i],next: curNode}}}reurn curNode 
}

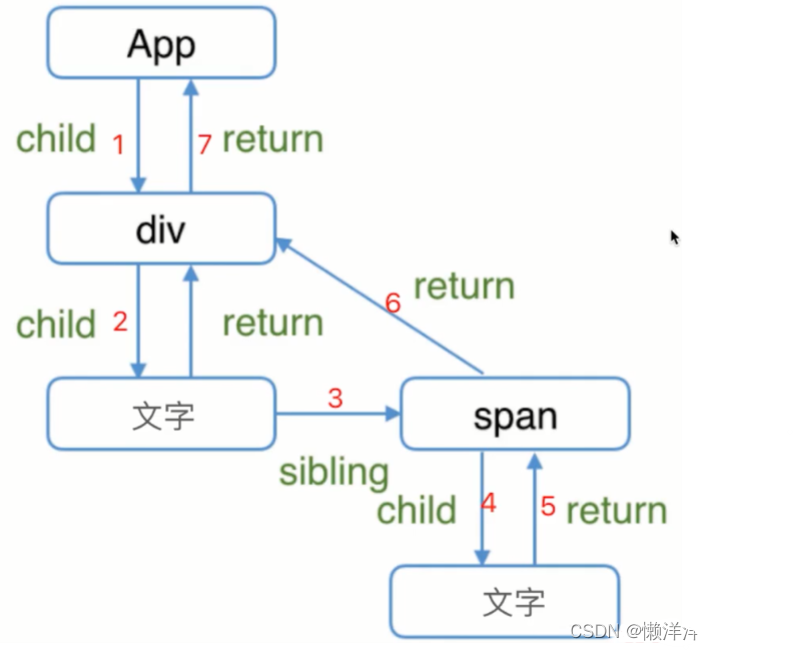
        链表在前端应用不多，例如React Fiber使用链表，通过将渲染树转换成链表表示，更灵活地控制渲染：

        在 React 16 中引入的 Fiber 架构使用链表数据结构来表示组件树，这样可以更好地控制组件树的遍历和更新过程。每个 Fiber 节点都包含了对应组件的信息以及与其他 Fiber 节点的关联关系，通过链表将这些 Fiber 节点连接起来形成一个虚拟的组件树。这种链表的结构使得 React 能够更灵活地控制组件更新的顺序，实现异步渲染和优先级调度等特性。

        使用链表而不是传统的递归方式遍历组件树，使得 React 能够实现更细粒度的控制，例如中断和恢复更新过程、优先级调度等。这种设计可以提高 React 应用的响应速度和用户体验，并且更好地支持 Suspense 和并发模式等新特性的引入。

4. 链表和数组，那个实现队列更快？

        数组是连续存储，push很快，shift很慢

        链表是非连续存储，add和delete都很快（但查找很慢）

        结论：链表实现队列更快

        链表实现队列

• 单向链表，但要同时记录head和tail
• 要从tail入队，从head出队，否则出队时tail不好定位
• length要实时记录，不可遍历链表获取（慢）

/**
* 用链表实现队列
*/
interface IListNode {value: numbernext: IListNode | null
}
class MyQueue {private head: IListNode | null = nullprivate tail: IListNode | null = nullprivate len = 0/*** 入队，在tail位置*/add(n: number) {const newNode: IListNode = {value: n,next: null,   // tail入队，结尾节点没next}// 处理headif (this.head == null) {this.head = newNode}// 处理tailconst tailNode = this.tailif (tailNode) {tailNode.next = nextNode}this.tail = newNodethis.len++}/*** 出队，在head的位置*/delete(): number | null {const headNode = this.headif (headNode = null) return nullif (this.len <= 0) return null// 取值const value = headNode.value// 处理headthis.head = headNode.next// 记录长度len--return value}get length(): number {return this.len  // length要单独存储，不能遍历链表来获取}
}

        链表和数组实现队列的性能对比

• 空间复杂度都是O(n)
• add时间复杂度：链表O(1)，数组O(1)；
• delete时间复杂度：链表O(1)，数组O(n)

数据结构的选择，要比算法优化更重要