网站建设都包括哪些方面建站模板平台

为了学习map和set的底层实现，需要知道红黑树，知道红黑树之前需要知道AVL树。
红黑树和AVL树都用到了二叉搜索树结构，所以先谈谈二叉搜索树。

1、二叉搜索树

二叉搜索树（Binary Search Tree）也称二叉排序树，它最重要的是能给数据排序以及去重。
其性质：

1. 若左子树不为空，左子树的键值都小于根以及右子树。
2. 若右子树不为空，右子树的键值都大于根以及左子树。
3. 二叉搜索树的子树都是二叉搜索树。

二叉搜索树顾名思义，根据其特性可以很方便让我们搜索一个值。
二叉树的中序遍历就是一个排序。
二叉搜索树的结点没有相同的值。

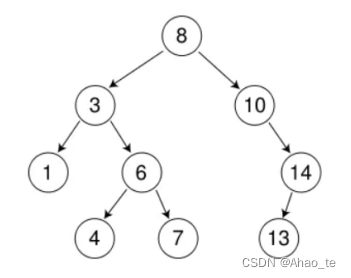
值得注意的是：

• 二叉搜索树没有要求严格平衡，所以查找一个值的时间复杂度最坏可能是O(N)（成为单枝树，就是一个链表。）
• 二叉搜索树不支持值修改，因为会打乱树的结构。

---

1.1 构建二叉搜索树

在二叉树的模型中，有K模型和KV模型，就是一个结点一个值和一个结点一个键值对两个模型。
一个值的很简单，而KV模型就是一个结点存放一个key和一个value。

下面实现的是KV模型的基本框架

#include <iostream>
#include <assert.h>
#include <string>
using namespace std;template<class K, class V>
struct BSTreeNode
{//设置成三叉链的结构，让子树能方便访问根结点struct BSTreeNode<K, V>* _left;struct BSTreeNode<K, V>* _right;struct BSTreeNode<K, V>* _parent;K _key;V _value;//构造BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _parent(nullptr), _key(key), _value(value){}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};

 

1.2 二叉搜索树的插入

二叉树插入很简单。
1、如果树是空，直接创建结点返回。
2、树不为空，根据搜索树的特性通过值的大小确定应该放在左还是右子树，如果到达空结点，那么就到达该放的位置。
3、确认好放的位置，因为需要链接，所以需要有一个parent能指向上一个结点。通过上一个结点和新结点的大小判断应该链接在哪边。
4、因为设计的是三叉链结构，所以最后还得指向父节点。

bool Insert(const K& key, const V& value){	//树为空if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = _root;//找到新结点应该放的位置while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//如果值相同直接返回return false;}}//确认好位置后，父子结点互相链接cur = new Node(key, value);if (parent->_key < cur->_key){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}return true;}

 

1.3 二叉搜索树的删除

	bool Erase(const K& key){//空树返回if (_root == nullptr){return false;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//先找到需要删的结点//删的结点左为空if (cur->_left == nullptr){//删的结点为根节点情况if (parent == cur){_root = cur->_right;}else{//需要确定父节点哪边指向curif (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//删的结点右为空//删的结点为根节点情况if (parent == cur){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}delete cur;}else{//左右都不为空,替换右子树最小的Node* minRight = cur->_right;while (minRight->_left){minRight = minRight->_left;}cur->_key = minRight->_key;cur->_value = minRight->_value;parent = minRight->_parent;//需要确定父节点哪边指向minRightif (parent->_right == minRight){parent->_right = minRight->_right;}else{parent->_left = minRight->_right;}//因为值交换了，所以删除右子树最小结点delete minRight;} //elsereturn true;} //else} // whilereturn false;} //Erase

 

1.4 二叉搜索树插入和删除的递归实现

有一点必须明确的是，非递归一定是比递归要好的，这里实现递归只是练习，增强代码能力。

首先是InOrder()方法的实现，当调用的方法是不含参数的，实现又需要有参数的，就可以再嵌套一层，并且_InOrder(Node* root)不想提供给类外调用，就可以放在私有域。

...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Insert(const K& key, const V& value){}bool Erase(const K& key){}void InOrder(){_InOrder(_root);}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}Node* _root = nullptr;
};

插入的递归实现

插入递归很简单，值得说的是，通过给root添加引用，能很方便的将新结点链接起来。

...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:...bool Insert(const K& key, const V& value){return _InsertR(_root, key, value);}bool Erase(const K& key){}...
private:...bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){//因为需要对root修改,所以在参数部分需要对root添加引用（Node*& root）root = new Node(key, value);return true;}if (root->_key < key){_InsertR(root->_right, key, value);}else if (root->_key > key){_InsertR(root->_left, key, value);}else{return false;}}Node* _root = nullptr;
};

删除的递归实现

删除的思路整体上和非递归差不多，不同的是。
1、因为删除需要改变树的结构，肯定是要改变每次递归的根节点的，所以需要传引用。
2、删除的思路是和右子树最小结点值交换后，删除最小结点。需要往右找到最小结点。

...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Erase(const K& key){_EraseR(_root, key);}
private:
...bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if(root->_key > key){return _EraseR(root->_left, key);}else{//找到删除的结点Node* del = root;if (root->_left == nullptr){//左边为空//因为要改变树的结构，改变root，所以root得加&//引用加完后，改变root也代表着改变父结点的指向//所以就是父节点指向root的指向变成指向root的右子树root = root->_right;}else if (root->_right == nullptr){//右边为空root = root->_left;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);// 转换成子树中去删除节点// 因为和最小节点的值交换后，原本root的值成了最小值// 再凭借key去查找最小值的结点删// 最小节点左边一定为空_EraseR(root->_right, key);}delete del;return true;} //else}Node* _root = nullptr;
};

本章完~