网站开发工程师绩效考核表seo培训机构
目录
二分图
染色法判定二分图
匈牙利算法
二分图
- 二分图,又叫二部图,将所有点分成两个集合,使得所有边只出现在集合之间的点之间,而集合内部的点之间没有边。
- 二分图当且仅当图中没有奇数环。只要图中环的边数没奇数个数的,它就是二分图。
- 二分图可以是连通的,也可以是不连通的
- 树一定二分图。

染色法判定二分图
题目如下:
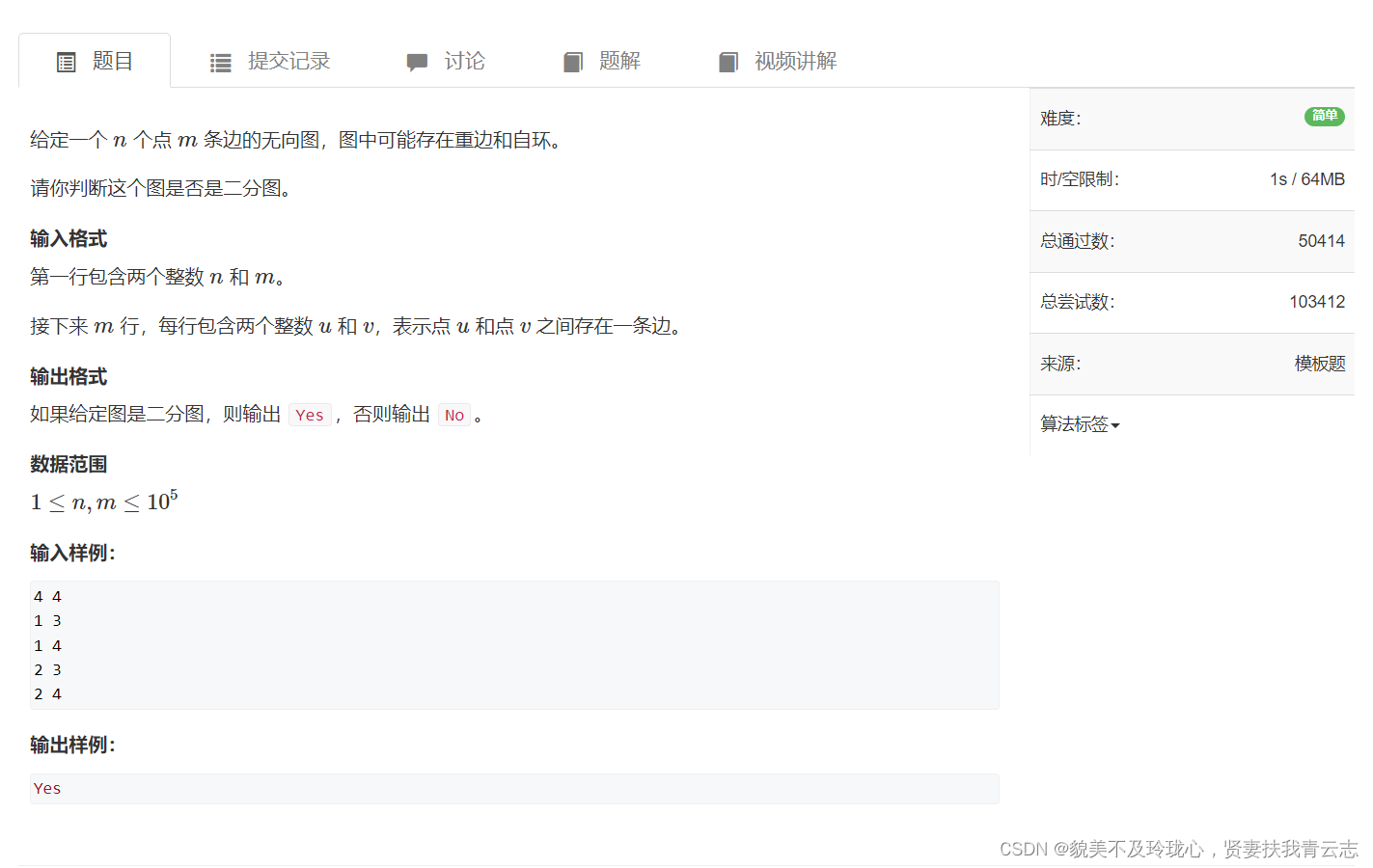
如果判断一个图是不是二分图?
- 开始对任意一未染色的顶点染色。
- 判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色。
- 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断。
- bfs和dfs可以搞定!
解题代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010 * 2;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int color[N];//保存各个点的颜色,0 未染色,1 是红色,2 是黑色
int n, m;//点和边void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}bool dfs(int u, int c)//深度优先遍历,参数1:点的编号 参数2:要染的颜色
{color[u] = c;//u的点成 c 染色//遍历和 u 相邻的点for(int i = h[u]; i!= -1; i = ne[i]){int b = e[i]; if(!color[b])//相邻的点没有颜色,则递归处理这个相邻点{if(!dfs(b, 3 - c)) return false;//(3 - 1 = 2, 如果 u 的颜色是2,则和 u 相邻的染成 1)//(3 - 2 = 1, 如果 u 的颜色是1,则和 u 相邻的染成 2)}else if(color[b] && color[b] != 3 - c)//如果已经染色,判断颜色是否为 3 - c{ return false;//如果不是,说明冲突,返回 }}return true;
}int main()
{memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i = 1; i <= n; i++)//遍历点{if(!color[i])//如果没染色{//以没染色的点为起点进行dfs搜索if(!dfs(i, 1))//染色该点,并递归处理和它相邻的点{cout << "No" << endl;//出现矛盾,输出NO return 0;}}}cout << "Yes" << endl;//全部染色完成,没有矛盾,输出YESreturn 0;
}算法板子:O(m+n),n表示点数,m表示边数
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{color[u] = c;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (color[j] == -1){if (!dfs(j, !c)) return false;}else if (color[j] == c) return false;}return true;
}bool check()
{memset(color, -1, sizeof color);bool flag = true;for (int i = 1; i <= n; i ++ )if (color[i] == -1)if (!dfs(i, 0)){flag = false;break;}return flag;
}匈牙利算法
题目如下:

解题代码
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 100010;int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, false, sizeof st);if (find(i)) res ++ ;}printf("%d\n", res);return 0;
}算法板子:O(m*n),n表示点数,m表示边数
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{memset(st, false, sizeof st);if (find(i)) res ++ ;
}
