用win2003做网站德阳网站seo
当涉及数学,有很多不同的话题可以讨论。你是否有特定的数学领域、概念或问题想要了解更多?以下是一些常见的数学领域和主题,你可以选择一个或者告诉我你感兴趣的具体内容,我将很乐意为你提供更多信息:
-
代数学: 包括代数方程、多项式、群论、环论等。
-
几何学: 从欧几里得几何到非欧几何,涉及空间、形状、位置等。
-
微积分: 研究变化率和积分,是分析学的基础。
-
概率与统计: 研究随机事件的概率和数据的分析。
-
数论: 研究整数的性质,包括素数、同余、数的分解等。
-
线性代数: 研究向量、矩阵、线性方程组等。
-
微分方程: 研究包含导数的方程,用于建模自然现象。
-
数学逻辑与集合论: 探讨命题、证明、集合的性质等。
-
离散数学: 包括图论、组合数学、逻辑等离散结构的研究。
-
应用数学: 数学在科学、工程、经济等领域的应用。
-
数学史: 探索数学的历史、数学家的贡献等。
历史背景
七桥问题源自欧拉(Leonhard Euler)在18世纪的研究。他在1736年首次提出了这个问题,通过解决这一问题,他为图论领域的创立奠定了基础。欧拉是瑞士数学家,以其在多个数学分支上的贡献而闻名,而七桥问题是他在图论领域最具影响力的作品之一。
问题描述
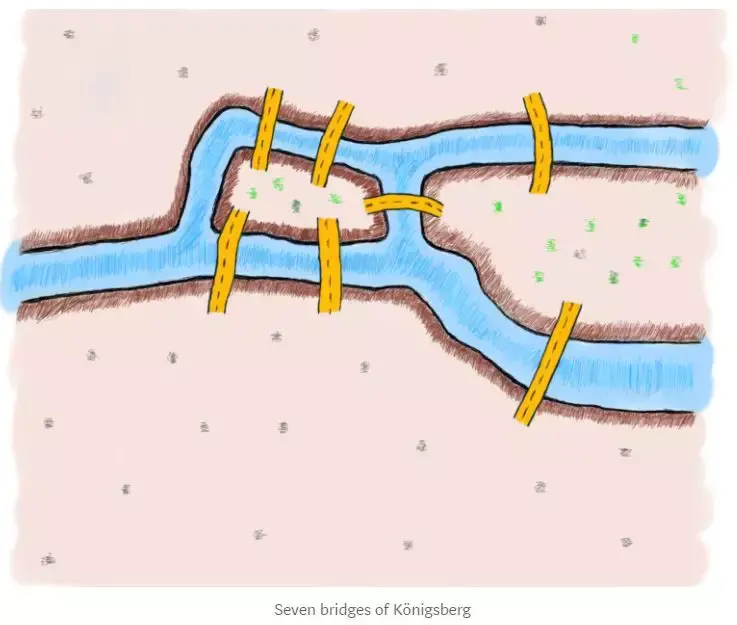
七桥问题的背景是庞特赫特里(现俄罗斯城市库尤比希夫)。这座城市由一座小岛和四个大陆组成,这些陆地和岛屿之间由七座桥连接。问题是,是否可能通过这些桥,恰好经过一次每座桥,将所有的陆地和岛屿连接起来,并且回到出发点,即起点。
解法与图论
欧拉通过抽象建模将七桥问题转化为图论问题,这是一种描述关系网络的数学方法。他将桥视为图中的边,陆地和岛屿视为图中的节点。这样,问题就变成了在图中找到一条路径,该路径通过每条边一次且仅一次,连接所有节点,并回到起点。
欧拉证明了,如果一个图中的节点的度数(连接边的数量)为奇数的节点数量是0或2,那么这个图可以有一个“欧拉路径”,即一条通过每条边一次且仅一次的路径。如果奇数度节点的数量超过2,那么没有欧拉路径。在七桥问题中,每个节点的度数都是奇数,因此无法找到满足条件的路径。
这一结论不仅解决了七桥问题,还奠定了图论领域的基础。欧拉路径和欧拉回路这些概念被广泛应用于电路设计、网络规划、交通优化等许多实际问题中。
影响与应用
七桥问题的解决对数学和其他领域产生了深远影响。首先,它标志着图论作为数学分支的诞生,图论成为了一种独立的数学领域,用于研究各种实际问题的抽象模型。其次,七桥问题展示了抽象建模和逻辑推理在解决复杂问题中的强大力量,这一思维方式在数学和科学研究中得到广泛应用。
此外,七桥问题也在教育领域有重要作用。它被广泛用作教学案例,帮助学生理解抽象数学概念和解决问题的方法。通过解决这个问题,学生能够培养逻辑思维、抽象建模和问题求解的能力。
总之,七桥问题不仅仅是数学史上的经典问题,更是一个启发性的故事,展示了数学思维如何在解决实际问题中发挥关键作用,以及如何为新的数学领域铺平道路。它在数学、教育和应用领域都具有重要意义。
当涉及图论时,我们在数学和计算机科学领域中遇到了一个有趣而重要的主题。图论研究的是图(Graph)这种抽象结构,它由节点(顶点)和连接节点的边组成。以下是一些图论的基本概念、应用和相关领域的介绍:
基本概念
-
图(Graph): 图是由一组节点和连接这些节点的边组成的抽象结构。图可以分为有向图和无向图,根据边是否有方向性。
-
顶点(Vertex): 图中的节点也被称为顶点,它们通常用来表示实体或对象。
-
边(Edge): 两个顶点之间的连接被称为边,边可以带有权重来表示节点间的关系强度。
-
度数(Degree): 对于无向图,一个顶点的度数是与它相连的边的数量。对于有向图,分为出度和入度,分别是从该顶点出发的边和指向该顶点的边的数量之和。
常见问题和概念
-
路径(Path): 顶点序列的一个序列,其中每个顶点通过一条边连接到下一个顶点。
-
环(Cycle): 至少包含三个顶点的路径,第一个和最后一个顶点相同,形成一个环。
-
连通性(Connectivity): 判断图中是否存在路径连接任意两个顶点。
-
最短路径(Shortest Path): 两个顶点之间的最短路径,可以通过各种算法找到,如迪杰斯特拉算法、弗洛伊德算法等。
应用领域
图论在许多领域都有广泛应用,包括但不限于:
-
网络分析: 用于分析社交网络、通信网络、互联网等的结构和关系。
-
交通规划: 优化道路、航班、列车线路等的设计和规划。
-
电路设计: 用于设计电子电路中的连接和布线。
-
排程问题: 解决任务分配、工作流程优化等问题。
-
生物学: 用于研究分子交互、蛋白质相互作用等。
-
优化问题: 在各种实际问题中,如资源分配、最优路径等。
相关领域
图论与许多其他数学和计算机科学领域紧密相关,包括:
-
组合数学: 图论中的许多问题涉及组合学的概念,如排列、组合等。
-
算法设计: 许多图论问题需要有效的算法来解决,如图的遍历、最短路径等。
-
计算机科学: 图数据结构在数据库、图数据库、编译器等领域有广泛应用。
