网站建设发展趋势昆明网站seo服务
傅里叶谱方法求解基本偏微分方程—一维波动方程
一维波动方程
对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 (−∞<x<∞)(-\infty<x<\infty)(−∞<x<∞) 弦的自由振动由式 (1)(1)(1) 描述。
∂2u∂t2=a2∂2u∂x2(1)\frac{\partial^2 u}{\partial t^2}=a^2 \frac{\partial^2 u}{\partial x^2} \tag{1} ∂t2∂2u=a2∂x2∂2u(1)
如果保证数值计算的区间足够大, 在一定时间内, 弦的振动范围始终没有超出计算区间 (或可以近似地这么认为), 那么就能够放心地使用周期性边界条件。取 a=1a=1a=1, 初始 条件为:
uut=0=2sech(x),∂u∂t∣t=0=0(2)u u_{t=0}=2 \operatorname{sech}(x),\left.\quad \frac{\partial u}{\partial t}\right|_{t=0}=0 \tag{2} uut=0=2sech(x),∂t∂ut=0=0(2)
在数学物理方法中, 无界弦的自由振动可由行波法求出解析解, 即达朗贝尔公式。 根据达朗贝尔公式, 从 t=0t=0t=0 开始, uuu 的初始状态 2sech(x)2 \operatorname{sech}(x)2sech(x) 将分裂为两个 sech 形的波, 分别向两边以速度 aaa 传播出去, 即正行波和反行波。下面用傅里叶缙方法求解无界弦 的自由振动问题, 并与达朗贝尔公式的预测进行比较。首先引入函数 vvv 对式 (1)(1)(1) 进行降阶:
{∂u∂t=v∂v∂t=a2∂2u∂x2(3)\left\{\begin{array}{l} \frac{\partial u}{\partial t}=v \\ \frac{\partial v}{\partial t}=a^2 \frac{\partial^2 u}{\partial x^2} \end{array}\right. \tag{3} {∂t∂u=v∂t∂v=a2∂x2∂2u(3)
对上式等号两边做傅里叶变换, 化为偏微分方程组:
{∂u^∂t=v^∂v^∂t=−a2k2u^(4)\left\{\begin{array}{l} \frac{\partial \hat{u}}{\partial t}=\hat{v} \\ \frac{\partial \hat{v}}{\partial t}=-a^2 k^2 \hat{u} \end{array}\right. \tag{4} {∂t∂u^=v^∂t∂v^=−a2k2u^(4)
这样就可以用 ode45 求解了, 详细代码如下:
主程序代码如下:
clear all; close all;L=80;N=256;
x=L/N*[-N/2:N/2-1];
k=(2*pi/L)*[0:N/2-1 -N/2:-1].';
% 初始条件
u=2*sech(x);ut=fft(u);
vt=zeros(1,N);uvt=[ut vt];
% 求解
a=1;t=0:0.5:20;
[t,uvtsol]=ode45('wave1D',t,uvt,[],N,k,a);
usol=ifft(uvtsol(:,1:N),[],2);
% 画图
p=[1 11 21 41];
for n=1:4subplot(5,2,n)plot(x,usol(p(n),:),'k','LineWidth',1.5),xlabel x,ylabel utitle(['t=' num2str(t(p(n)))]),axis([-L/2 L/2 0 2])
end
subplot(5,2,5:10)
waterfall(x,t,usol),view(10,45)
xlabel x,ylabel t,zlabel u,axis([-L/2 L/2 0 t(end) 0 2])文件 wave1D.m 代码如下:
function duvt=wave1D(t,uvt,dummy,N,k,a)
ut=uvt(1:N);vt=uvt(N+[1:N]);
duvt=[vt;-a^2*(k).^2.*ut];
end
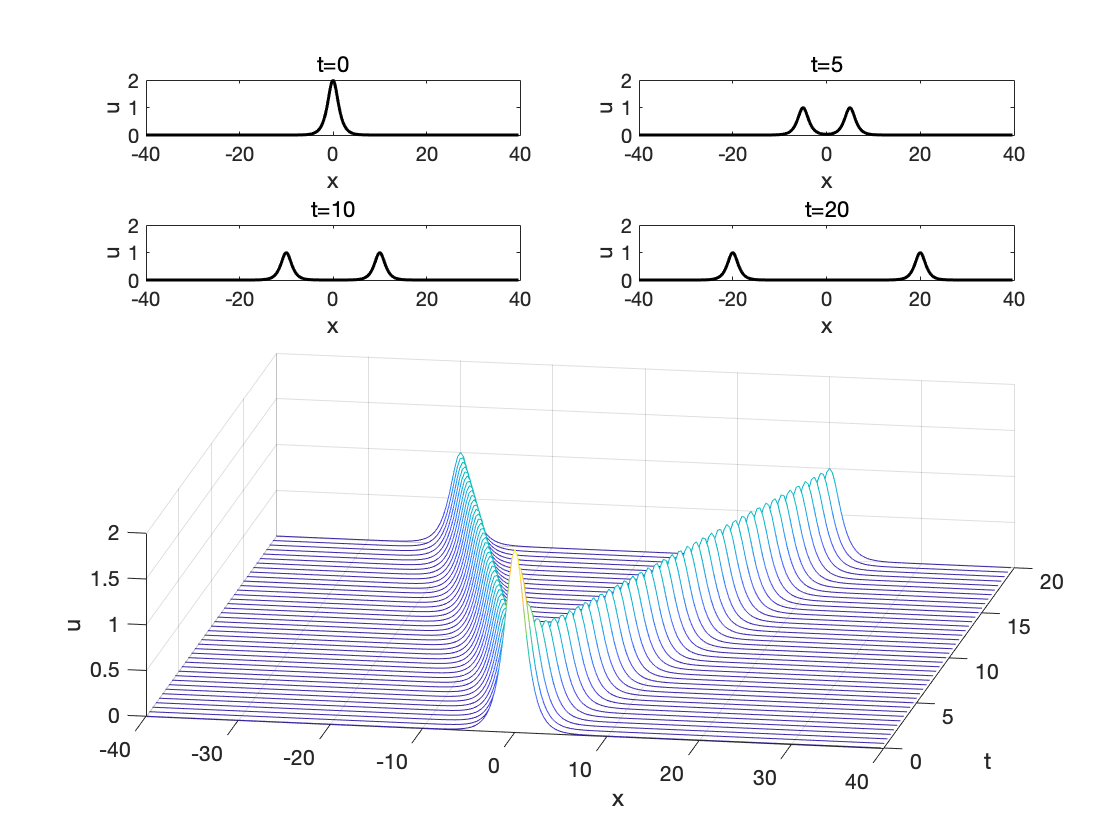
计算结果如图所示, 初始状态的波形分裂成两半, 并分别向 xxx 轴正方向和负方向 以速度 aaa 运动, 这和达朗贝尔公式给出的结论是一致的。