福建省住房和城乡建设厅门户网站东莞seo优化推广

前言

STK软件在给定六根数时，可求得卫星位置和速度矢量，但有时我们通过星历参数得到卫星的位置和速度矢量，希望能够反演得出卫星轨道的六根数。从而方便对该卫星轨道进行仿真模拟。

计算过程

给定卫星在J2000坐标系下的的位置矢量r和速度矢量v

1. 利用卫星动量矩计算轨道倾角和升交点赤径
   计算卫星相对于地心的动量矩，该动量矩等于卫星地心矩矢量和速度矢量的矢积：$\text{h}=\text{r}\times \text{v}$，动量矩的方向和卫星轨道面的法线是平行的，动量矩和Z轴夹角为轨道倾角$i$，轨道平面和地球赤道平面的交线为节线ON；节线ON与X轴夹角为升交点赤径$\Omega$，$(i,\Omega )$确定了轨道平面在空间坐标系中的方位。
   $$i=arccos(h_x/h),\Omega =arctan(-h_x/h_y)$$
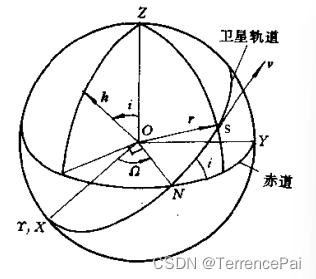
2. 利用卫星机械能计算轨道半长轴
   $$E=v^2/2-\mu /r,E=-\mu /2a$$
   其中$h$为动量矩模值，$\mu$为引力常量：398600.44
   $k{m}^3/s^2$，$v$为速度矢量模值，$r$为位置矢量模值，$a$为椭圆轨道半长轴。
3. 利用轨道半通经和轨道半长轴计算椭圆轨道偏心率
   $$p=h^2/\mu ,e=\sqrt{(1-(p/a))}$$
   其中，$p$为半通径，$e$为偏心率。
4. 利用偏心率、半通经和位置矢量模值计算真近点角
   $$f=arccos(p-r)/re$$
5. 利用真近点角和升交点幅角计算近地点辐角
   $$\omega =u-f,u=arccos(\text{ON}\cdot \text{r}/(r\ast ON))$$
   其中，升交点幅角为节线ON矢量与卫星位置矢量的夹角。
   $\text{ON}=(cos\Omega ,sin\Omega ,0)$。

代码实现

具体计算时，需要考虑反三角函数的值域与实际情况对应。

#include <string>
#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;
const double mu{ 398600.44 };//引力常数:(km)3/s2
const double PI{ acos(-1) };//PI
const double rad2deg{ 180.0 / PI };//PI
#define ABS(x) (sqrt((x)[0]*(x)[0]+(x)[1]*(x)[1]+(x)[2]*(x)[2]))
struct OrbitParm {double inclination{ };       //轨道倾角:degdouble RAAN{ };             //升交点赤经:deg    :计算结果差180double semimajorAxis{};     //半长轴:km  6917.21double Eccentricity{};    //偏心率:double argumentOfPerigee{};  //近地点辐角:deg  :double trueAnomaly{  };  //真近点角 ：主要考虑什么时候要对称变换，因为acos只能输出0—pi，而目标区间范围0—2pi
};
struct Motion {//J2000double location[3]{};   //位置:x、y、z  kmdouble speed[3]{};                //速度:x、y、z  km/sec  
};
OrbitParm motionOrbitParmConvert(Motion mot) {//to be done//卫星相对于地心的动量矩:h=r*v（矢量的矢积）double h[3]{ mot.location[1] * mot.speed[2] - mot.location[2] * mot.speed[1], \- mot.location[0] * mot.speed[2] + mot.location[2] * mot.speed[0], \mot.location[0] * mot.speed[1] - mot.location[1] * mot.speed[0] };double absH{ ABS(h) };OrbitParm opa{};opa.inclination = acos(h[2] / absH) * rad2deg;opa.RAAN = atan2(h[0], -h[1]) * rad2deg;if ((opa.RAAN) < 0)//目标区间为0—2piopa.RAAN = opa.RAAN + 360;double p{ absH * absH / mu };     //椭圆轨道的半通径double absR{ ABS(mot.location) };double absV{ ABS(mot.speed) };double E = absV * absV / 2.0 - mu / absR; //卫星的机械能Eopa.semimajorAxis = -mu / E / 2.0;//半长轴由机械能决定opa.Eccentricity = sqrt(1 - p / opa.semimajorAxis);//偏心率可通过半长轴和半通径联合求得opa.trueAnomaly = acos((p - absR) / absR / opa.Eccentricity) * rad2deg;if (1)//主要考虑什么时候要对称变换，因为acos只能输出0—pi，而目标区间范围0—2piopa.trueAnomaly = 360 - opa.trueAnomaly;double u[3] = { cos(opa.RAAN / rad2deg),sin(opa.RAAN / rad2deg),0 };opa.argumentOfPerigee = acos((u[0] * mot.location[0] + u[1] * mot.location[1]) / absR) * rad2deg;opa.argumentOfPerigee -= opa.trueAnomaly;if (opa.argumentOfPerigee < 0)opa.argumentOfPerigee += 360;return opa;
}
Motion motionOrbitParmConvert(OrbitParm opa) {//暂时不编return{};
}
int main()
{//输入示例，第一个大括号依次填入J2000坐标系下的xyz位置，第二个括号依次填入J2000坐标系下的xyz速度auto opa = motionOrbitParmConvert({ {-3904.3,-4663.0,3290.863664} , {1.4,3.4,6.6} });cout <<right <<fixed << setprecision(6)<<setfill('0');cout << setw(11) << opa.inclination << endl;cout << setw(11) << opa.Eccentricity << endl;cout << setw(11) << opa.semimajorAxis << endl;cout << setw(11) << opa.RAAN << endl;cout << setw(11) << opa.trueAnomaly << endl;cout << setw(11) << opa.argumentOfPerigee << endl;return 0;
}

运行结果

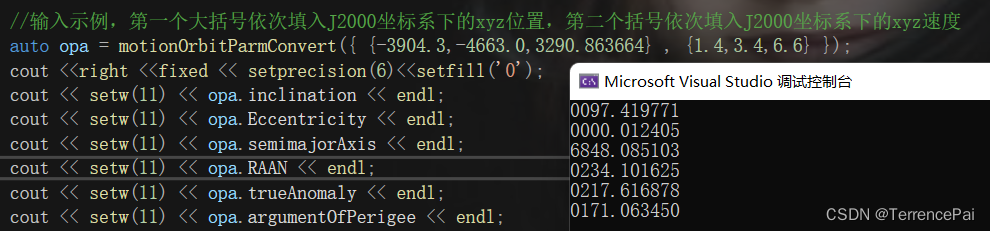
更新

除了计算六根数，还计算了平近点角、偏近点角

class Orbit_Para_Object
{
public://卫星半长轴double dOrbit_a;//计算轨道偏心率double dOrbit_e;//计算轨道偏心角double dOrbit_E1;//计算真近心角double dOrbit_Theta;//计算平均近心角double dOrbit_M;//计算轨道倾角double dOrbit_Angle_Inclination;//升交点赤经double dOrbit_Angle_Omig;//近地点幅角double dOrbit_Angle_W;protected:private:};#define ABS(x) (sqrt((x)[0]*(x)[0]+(x)[1]*(x)[1]+(x)[2]*(x)[2]))
const double rad2deg{ 180.0 / pi };//PI
Orbit_Para_Object Cal_orbit_info(double sat_x_g, double sat_y_g, double sat_z_g, double sat_vx_g, double sat_vy_g, double sat_vz_g, double Gravitation_P) {//to be done//  //卫星相对于地心的动量矩:h=r*v（矢量的矢积）//J2000double location[3]={ sat_x_g,sat_y_g,sat_z_g };   //位置:x、y、z  kmdouble speed[3]={ sat_vx_g,sat_vy_g,sat_vz_g };                //速度:x、y、z  km/sec  double h[3]={location[1] * speed[2] - location[2] * speed[1], \- location[0] * speed[2] + location[2] * speed[0], \location[0] * speed[1] - location[1] * speed[0] };double absH{ ABS(h) };Orbit_Para_Object opa{};opa.dOrbit_Angle_Inclination = acos(h[2] / absH) * rad2deg;opa.dOrbit_Angle_Omig = atan2(h[0], -h[1]) * rad2deg;if ((opa.dOrbit_Angle_Omig) < 0)//目标区间为0—2piopa.dOrbit_Angle_Omig = opa.dOrbit_Angle_Omig + 360;double p = { absH * absH / Gravitation_P };     //椭圆轨道的半通径double absR = { ABS(location) };double absV = { ABS(speed) };double E = absV * absV / 2.0 - Gravitation_P / absR; //卫星的机械能Eopa.dOrbit_a = -Gravitation_P / E / 2.0;//半长轴由机械能决定opa.dOrbit_e = sqrt(1 - p / opa.dOrbit_a);//偏心率可通过半长轴和半通径联合求得opa.dOrbit_Theta = acos((p - absR) / absR / opa.dOrbit_e) * rad2deg;if (1)//主要考虑什么时候要对称变换，因为acos只能输出0—pi，而目标区间范围0—2piopa.dOrbit_Theta = 360 - opa.dOrbit_Theta;double u[3] = { cos(opa.dOrbit_Angle_Omig / rad2deg),sin(opa.dOrbit_Angle_Omig / rad2deg),0 };opa.dOrbit_Angle_W = acos((u[0] * location[0] + u[1] * location[1]) / absR) * rad2deg;opa.dOrbit_Angle_W -= opa.dOrbit_Theta;if (opa.dOrbit_Angle_W < 0)opa.dOrbit_Angle_W += 360;double n=sqrt( Gravitation_P/( opa.dOrbit_a * opa.dOrbit_a * opa.dOrbit_a));//卫星沿椭圆轨道运行的平均速率//计算偏近点角//opa.dOrbit_E1 = acos(absR * cos(opa.dOrbit_Theta) / opa.dOrbit_a + opa.dOrbit_e);opa.dOrbit_E1 = atan2(sqrt(1-opa.dOrbit_e* opa.dOrbit_e* opa.dOrbit_e) *sin(opa.dOrbit_Theta)/(1+opa.dOrbit_e*cos(opa.dOrbit_Theta)), (opa.dOrbit_e + cos(opa.dOrbit_Theta)) / (1 + opa.dOrbit_e * cos(opa.dOrbit_Theta)));//计算平近点角opa.dOrbit_M =fmod((opa.dOrbit_E1- opa.dOrbit_e*sin(opa.dOrbit_E1)) * rad2deg,360 );opa.dOrbit_E1 *= rad2deg;if (opa.dOrbit_E1 < 0)opa.dOrbit_E1 += 360;if (opa.dOrbit_M < 0)opa.dOrbit_M += 360;return opa;}

总结

该文实现了通过卫星星历参数反演得出卫星轨道的六根数。