成都公司做网站多少钱在百度上做广告推广要多少钱

通常用“帮派”的例子来说明并查集的应用背景：在一个城市中有 $n(n<10^6)$个人，他们分成不同的帮派，给出一些人的关系，例如： $1$号、 $2$号是朋友； $1$号、 $3$号也是朋友，那么他们都属于一个帮派。在分析完所有的朋友关系之后，问有多少帮派，每人属于哪个帮派。

这个数据量应该是不能用暴力的办法求解，那我们应该怎么办呢？
由此，我们引出一种新的数据结构：并查集

1.并查集操作的简单实现

1. 初始化:
   定义数组 $ints[]$ 是以结点 $i$ 为元素的并查集，在开始的时候还没有处理点与点之间的朋友关系，所以每个点属于独立的集，并且以元素 $i$ 的值表示它的集 $s[i]$，例如元素 $1$的集$s[1]=1$。所示为图解，左边给出了元素与集合的值，右边画出了逻辑关系。为了便于讲解，左边区分了结点 $i$ 和集 $s$ (把集的编号加上了下画线)；右边用圆圈表示集，方块表示元素。
   
2. 合并(1):
   例如加入第 1 个朋友关系$(1,2)$，如下图所示。在并查集s中，把结点 1 合
   并到结点 2，也就是把结点 1 的集 1 改成结点 2 的集 2 。
3. 合并(2):
   加入第 $2$ 个朋友关系$(1,3)$，如下图所示。查找结点 $1$ 的集是 $2$ ,再递归查找元素 $2$ 的集是$2$ ,然后把元素 $2$ 的集 $2$ 合并到结点 $3$ 的集 $3$ 。此时，结点 $1$、$2$、$3$属于一个集。在图中，为了简化图示，把元素 $2$ 和集 $2$ 画在了一起。
   
4. 合并(3)：
   加入第 $3$ 个朋友关系$(2,4)$, 如图所示。
   
5. 查找：
   在上面步骤中已经有查找操作。查找元素的集是一个递归的过程，直到元素的值和它的集相等就找到了根结点的集。从上面的图中可以看到，这棵搜索树的高度可能很大，复杂度是$O_{(n)}$的，变成了一个链表，出现了树的“退化”现象。
6. 统计有多少个集:
   如果 $s[i]=i$，这是一个根结点，是它所在的集的代表。统计根结点的数量，就是集的数量。

2.解决问题

有 $n$ 个人一起吃饭，有些人互相认识。认识的人想坐在一起，不想跟陌生人坐。例如 $A$ 认识$B$，$B$ 认识$C$，那么 $A$、$B$、$C$会坐在一张桌子上。给出认识的人的关系，问需要多少张桌子。

我们可以根据上文的描述，得到如下并查集代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1007;
int f[N];  //并查集void init(){  //初始化for(int i = 1; i <= N; i++){f[i] = i;}
}int find_father(int x){  //找自己的集if(f[x] == x)return x;else return find_father(f[x]);
}void union_set(int x, int y){  //合并x = find_father(x);y = find_father(y);if(x != y)f[x] = f[y];
}
int main(){init();int n, m, x, y;cin >> n >> m;for(int i = 1; i <= m; i++){cin >> x >> y;union_set(x, y);}int cnt = 0;  //记录集的数量for(int i = 1; i <= n; i++){if(f[i] == i){cnt ++;}}cout << cnt;return 0;
}

在上述程序中，查找、合并、的搜索深度是树的长度，复杂度都是 $O_{(n)}$，性能比较差。下面介绍合并和查找的优化方法，优化之后，查找和合并的复杂度都小于$O(lo{g}_{2}n)$。

3. 并查集优化

3.1 合并的优化

在合并元素$x$和$y$时先搜到它们的根结点，然后再合并这两个根结点，即把一个根结点的集改成另一个根结点。这两个根结点的高度不同，如果把高度较小的集合并到较大的集上，能减少树的高度。下面是优化后的代码，在初始化时用 $height[i]$ 定义元素 $i$ 的高度，在合并时一同更改。

int high[N];
void init(){  //初始化for(int i = 1; i <= N; i++){f[i] = i;high[i] = 0;}
}
void union_set(int x, int y){  //优化合并x = find_father(x);y = find_father(y);if(high[x] == high[y]){high[x]++;f[y] = x;}else{if(high[x] < high[y]){f[x] = y;}else{f[y] = x;}}
}

3.2查询优化

在上面的查询程序 $fin{d}_{f}ather()$ 中，查询元素 $i$ 所属的集需要搜索路径找到根结点，返回
的结果是根结点。这条搜索路径可能很长。如果在返回的时候顺便把 $i$ 所属的集改成根结
点，如图所示，那么下次再搜的时候就能在 $O_{(1)}$ 的时间内得到结果。

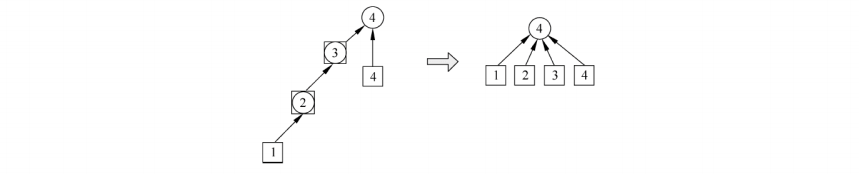
int find_father(int x){ //优化的查询 if(f[x] != x)f[x] = find_father(f[x]);  return f[x];  
}

这个方法称为路径压缩，因为在递归过程中，整个搜索路径上的元素（从元素 $i$ 到根结点的所有元素）所属的集都被改为根结点。路径压缩不仅优化了下次查询，而且优化了合并，因为在合并时也用到了查询。

3.3查询优化2

上面的代码用递归实现，如果数据规模太大，担心爆栈，可以用下面的非递归代码：

int find_father(int x) {int r = x;while (f[r] != r)r = f[r];  //找到根的位置int i = x, j;while(i != r){j = f[i];f[i] = r;  //把路径的根统一i = j;}return r;
}