专业积分商城网站建设怎么样在百度上推广自己的产品
一.记忆化搜索概述
1.概念
搜索是一种简单有效但是效率又很低下的算法结构,其低效的原因主要在于存在很多重叠子问题。而记忆化搜索则是在搜索的基础上,利用数组来记录已经计算出来的重叠子问题状态,进行合理化的剪枝,从而降低时间复杂度。这个记录状态的过程就是记忆化的过程,我们需要找到不同搜索层次之间的子问题、状态转移关系,这与动态规划的思想又不谋而合。
简单来说,记忆化搜索是一种典型的空间换时间的思想,记忆化搜索 = 深度优先搜索实现 + 动态规划思想(记录状态、剪枝)。
2.图示
此处以某个记忆化搜索题目的结构树为例。在搜索过程中,我们将问题的搜索树画出来如下所示。左侧为暴力搜索的搜索树,而右侧为记忆化搜索剪枝的搜索树。
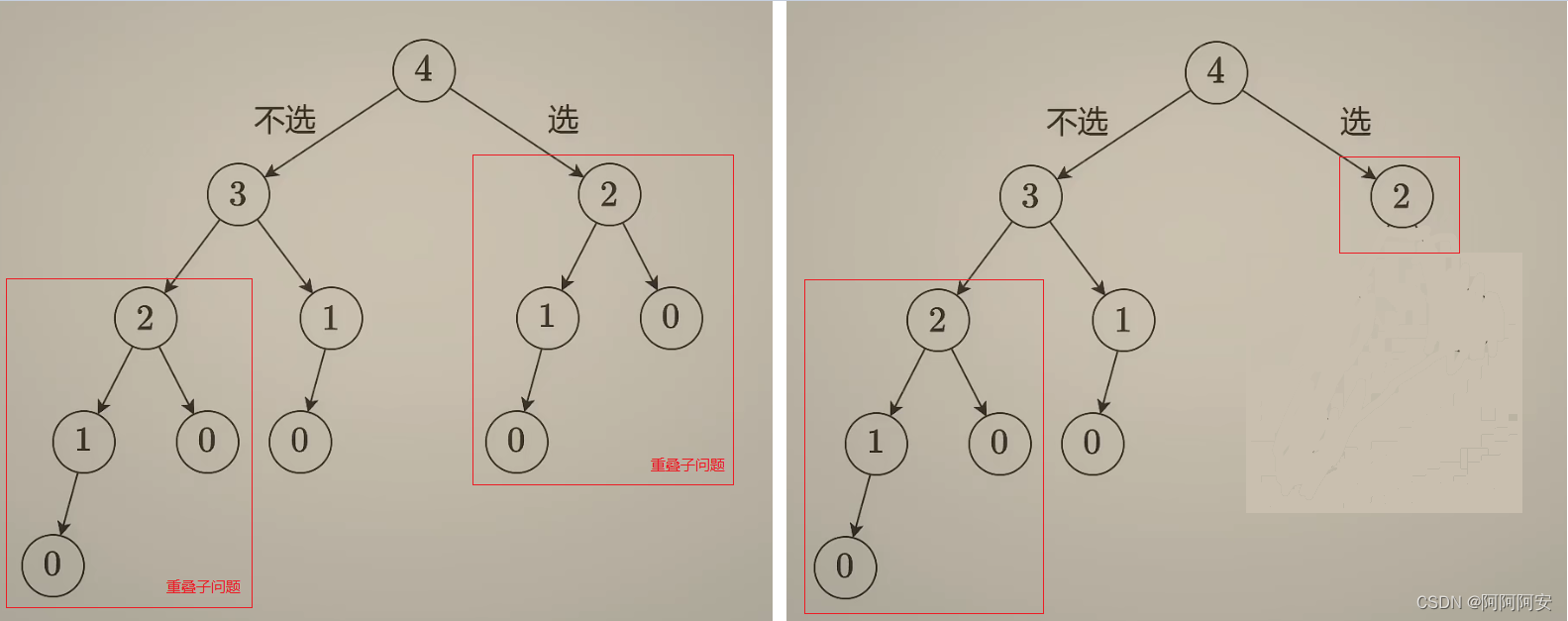
记忆化搜索可以看作是动态规划的前置过程,或者说记忆化搜索一般是自顶向下的,而动态规划一般是自底向上的。
二.例题
1.LeetCode 45. 跳跃游戏改
给定一个长度为 n 的整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处(0 <= j <= nums[i])
返回到达
nums[n - 1]的最小跳跃次数。已知跳跃次数有上限K,若无法在K次内到达则返回 -1
(1)记忆化搜索
对于该题,我们可以先求出到达终点的最小跳跃次数 t,然后比较 t 与上限 K 的大小,若t > K则返回 -1 。
按照搜索的思想来说,我们在到达某个索引 i 时,该位置到达终点的最小跳跃次数取决于 min(dfs(i) , dfs(i+j) + 1),0 <= j <= nums[i] ;按照记忆化的思想,像最短路一样,某个位置 i 到达终点的最小跳跃次数应该是确定的,属于重叠子问题,不应该重复搜索,因此可以使用数组记录每个位置的最小次数。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10000 + 7;
int n,k,nums[maxn],mem[maxn];int dfs(int index){if(index >= n-1)return 0;if(mem[index]!=-1)return mem[index];//记忆化int ans = -1;for(int i = 1;i<=nums[index];i++){int res = dfs(index+i)+1;if(res != 0){ans = ans==-1?res:min(ans,res);}}return mem[index] = ans;
}int main()
{memset(mem,-1,sizeof(mem));scanf("%d%d",&n,&k);for(int i = 0;i<n;i++){scanf("%d",&nums[i]);}dfs(0);if(mem[0] == -1 || mem[0] > k)printf("-1\n");else printf("%d\n",mem[0]);
}
(2)贪心
记忆化搜索的方式可行,但是复杂度还是有点高会超时。我们重新来审视这个题,每个位置处的跳跃距离是固定的、相互独立的,与之前的子节点和之后的子节点都是没关系的,也就是说该题其实与动态规划思想无关。
考虑现在跳到了位置 i ,那么接下来应该选择跳到 i+1 ~ i+nums[i] 的哪个位置呢?答案是「贪心」地选择能跳跃到距离最后一个位置最远的那个位置(即使得“探索序列”能够拓宽最远的那个位置),原因是以该位置为下一次起跳点所能到达的地方,由于其是最远的,所以能够覆盖其他所有的起跳点位置范围,这肯定是最优的。
当一次 跳跃 结束时,从下一个格子开始,到现在 能跳到最远的距离,都 是下一次 跳跃 的 起跳点。所以跳完一次之后,不断更新维护下一次 起跳点的范围。在新的范围内跳,更新 能跳到最远的距离。
int jump(int len){int ans = 0;int start = 0,last = 0; //初始起跳范围 [0,0] 闭区间while(last < len - 1){int maxpos = 0;//选择下一次跳哪个for(int i = start;i<=last;i++){maxpos = max(maxpos,i+nums[i]);}start = last+1; // 下一次起跳点范围开始的格子last = maxpos; // 下一次起跳点范围结束的格子ans++; // 跳跃次数}return ans;
}
2. 青蛙过河
一只青蛙想要过河。 假定河流被等分为若干个单元格,并且在每一个单元格内都有可能放有一块石子(也有可能没有)。 青蛙可以跳上石子,但是不可以跳入水中。
假设河流中一共有 n 个石子,给你每个石子的河流单元格位置的列表 stones(用单元格序号升序表示), 请判定青蛙能否成功过河(即能否在最后一步跳至最后一块石子上)。
开始时, 青蛙默认已站在第一块石子上,并可以假定它第一步只能跳跃一个单位(即只能从单元格1 跳至单元格 2 )。如果青蛙上一步跳跃了 k 个单位,那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意,青蛙只能向前方(终点的方向)跳跃。
输入:stones = [0,1,3,5,6,8,12,17] 输出:true 解释:青蛙可以成功过河,按照如下方案跳跃:跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后,跳 5 个单位到第 8 个石子(即最后一块石子)。
该题题意与上一题的跳跃游戏类似,但是二者很大的一个不同就是每个位置的跳跃范围:跳跃游戏中每个位置的跳跃范围是固定的、相互独立的,而该题中每个位置的跳跃范围受到上一次跳跃的影响,具有子结构,因此该题优先考虑动态规划或记忆化搜索。
对于记忆化搜索来说,我们可以仍然去搜索所有可能的路径。但是对于每个节点来说,他的状态主要受到两个因素的影响:当前所在 stone 下标位置、上一次跳的步长,这两个因素决定了该位置后续的最优解。因此我们可以使用一个二维数组 dp[i][j] 保留位置 i 时,上个步长为 j 时的能否到达状态,以此进行记忆化搜索。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10000 + 7;
int n,stones[maxn];
vector<unordered_map<int, bool>> dp;bool dfs(int index,int preSteps){if(index == n-1)return true;if(index >= n)return false;if(dp[index].count(preSteps))return dp[index][preSteps];bool res = false;for(int i = preSteps-1;i<=preSteps+1;i++){if(i<=0)continue;int nextpos = lower_bound(stones+index, stones+n, stones[index]+i) - stones;if(nextpos < n && stones[nextpos] == stones[index]+i){res = dfs(nextpos,i);if(res)break;}}return dp[index][preSteps] = res;
}int main()
{scanf("%d",&n);dp.resize(n); // 初始化 vector 空间长度,int默认填充0,此处默认填充 空mapfor(int i = 0;i<n;i++){scanf("%d",&stones[i]);}bool ans = dfs(0,0);if(ans)printf("true\n");else printf("false\n");return 0;
}